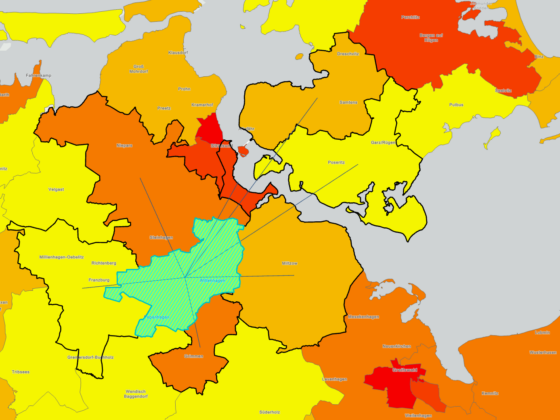
Die Interpolation ist eine weit verbreitete Methode in der räumlichen Analyse und der Geostatistical Analyst ein ideales Werkzeug dafür.
Anhand verschiedener Ansätze können mit dem Geostatistical Analyst kontinuierliche Oberflächen basierend auf gemessenen Werten vorhergesagt werden, beispielsweise die Nitratkonzentration auf einem Feld, die Ozonkonzentration in der Atmosphäre oder die Wasserqualität in Seen.
Die verschiedenen Interpolations-Methoden für räumliche Daten teilen wir in die zwei groben Klassen „deterministische“ und „geostatistische“ Methoden ein. Deterministische Methoden verwenden mathematische Funktionen, um Werte zu interpolieren. Geostatistische Methoden vereinen mathematische und statistische Methoden, um einerseits die Werte zu interpolieren und andererseits die Unsicherheit der Vorhersage zu beurteilen. Im Gegensatz zu den deterministischen Methoden wird dabei eine räumliche Autokorrelation angenommen, d.h. Messwerte die nahe beieinander liegen sind sich ähnlicher als Messwerte, die weit auseinander liegen.
Mit dem Geostatistical Analyst kann sowohl anhand deterministischer (z.B. IDW, Radial Basis Functions) als auch geostatistischer (Kriging) Methoden interpoliert werden. Er beinhaltet zwei Komponenten: die Geostatistical Analyst Toolbox und den Geostatistical Wizard. Beide zusammen bieten Tools, um die Daten für die Interpolation vorzubereiten, eine passende Methode auszuwählen und das Resultat der Interpolation im Anschluss zu validieren. Der Wizard führt die Benutzer:innen durch die Interpolation, sobald eine passende Methode ausgewählt worden ist.
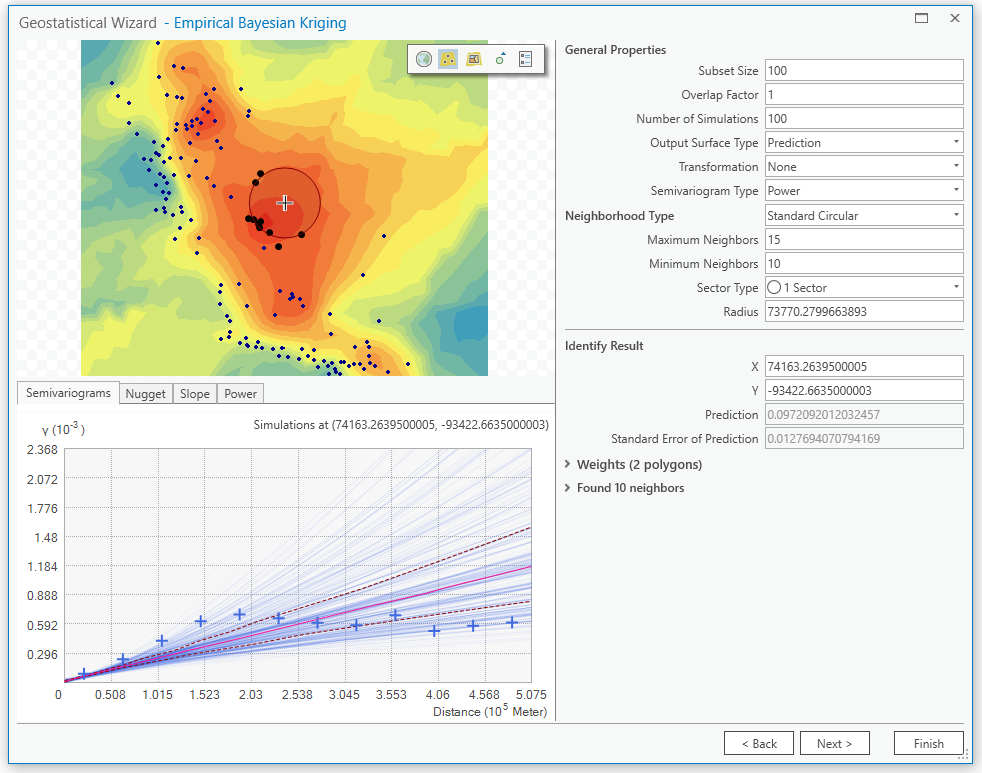
Je nach Interpolationsmethode stehen den Benutzer:innen im Prozess verschiedene Möglichkeiten zur Verfügung, um die Daten zu normalisieren sowie Trends und Cluster in den Daten zu berücksichtigen.
Viele Interpolations-Methoden, insbesondere das Kriging, setzen einiges an Wissen voraus. Parameter müssen manuell angepasst werden, um eine optimale Interpolation zu erhalten. Das Werkzeug Empirical Baysian Kriging (EBK) hingegen können Sie auch verwenden, ohne ein Spezialist auf dem Gebiet der Interpolation zu sein. EBK übernimmt den komplizierten Teil der Parametrisierung durch die Simulierung vieler verschiedener Semivariogramme.
Das Werkzeug EBK Regression Prediction berücksichtigt zusätzlich zur EBK-Modellierung Rasterdaten als erklärende Variablen. Beispielsweise kann für die Interpolation von Wohnungsmietpreisen ein Raster mit Informationen zur Lärmbelastung berücksichtigt werden.
Gerade im Bereich von Umwelterhebungen in Ozeanen oder der Atmosphäre kommt es vor, dass Messwerte nicht nur in einer Tiefe bzw. Höhe erhoben werden, sondern in 3D. Hier bietet der Geostatistical Analyst das Werkzeug „Empirical Bayesian Kriging 3D“, mit welchem Punktwolken in 3D interpoliert werden können, was für die Modellierung von Prozessen in Ozeanen oder der Atmosphäre interessant ist. Eine 3D-Interpolation kann aber auch im zeitlichen Verlauf erfolgen und anschließend beispielsweise als Voxel-Layer dargestellt werden. Die Zeit wird dabei durch die Höhe abgebildet. Die Abbildung 2 zeigt ein solches Interpolationsresultat. Als Basis dienten dabei Ozonmesswerte über mehrere Jahre, die in Raum und Zeit interpoliert wurden.

Mit den beiden Werkzeugen „Kernel Interpolation With Barriers“ und „Diffusion Interpolation With Barriers“ ist es außerdem möglich, Barriere-Features anzugeben, welche in der Interpolation berücksichtigt werden.
Lizenzierung
Der Geostatistical Analyst ist eine Erweiterung von ArcGIS Pro und über die Geostatistical Analyst-Lizenz verfügbar.